Numerical Methods for First Order Differential Equations
Most ODEs in real-world problems cannot be solved exactly; but there are various methods that can give us an accurate answer.
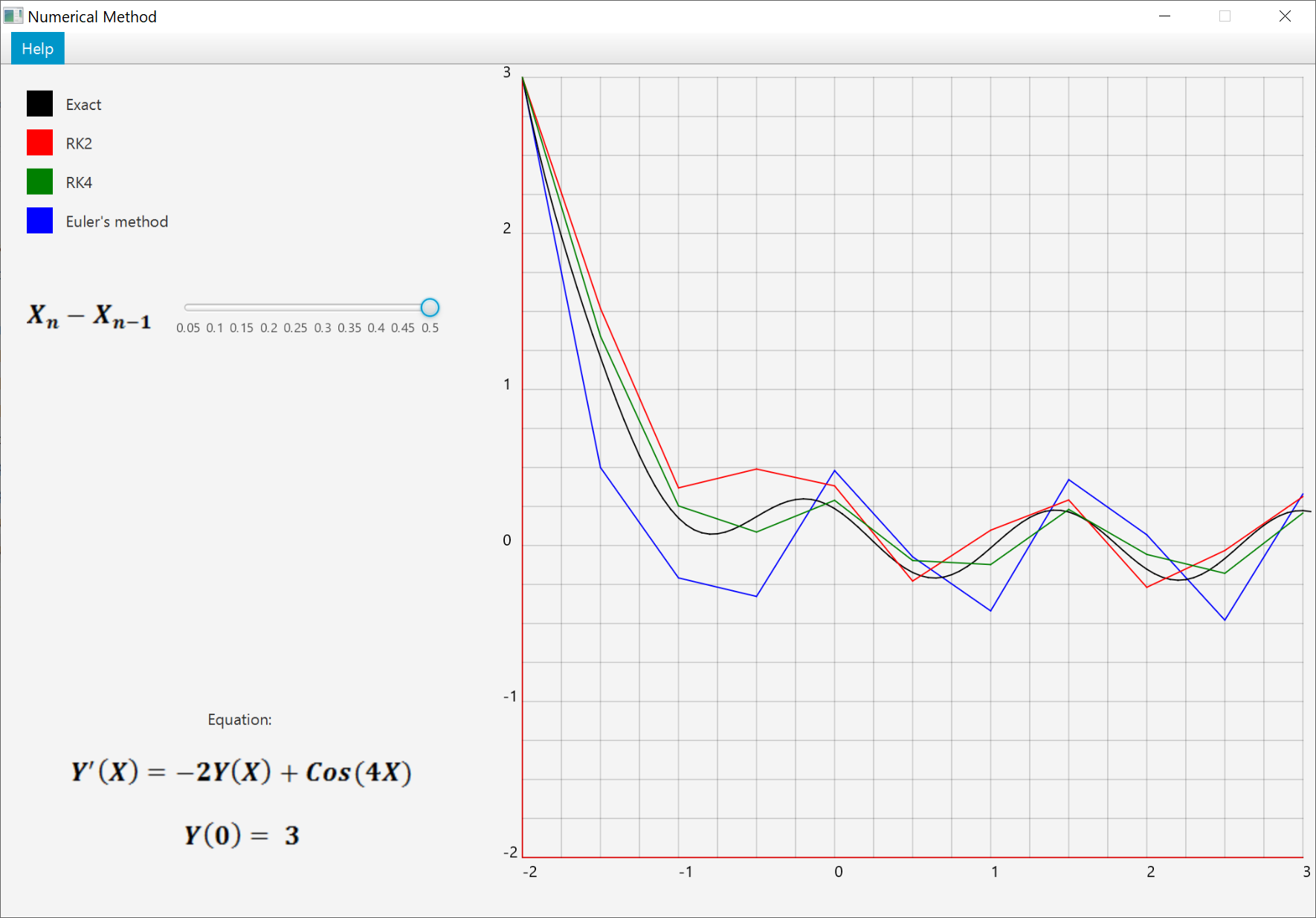
Numerical methods can be used to get an accurate approximation to an ODE. There are different
approaches for getting this approximation; few of them are shown as examples in this tool: Euler’s
method, second order Runge-Kutta method (RK2) with midpoint approach and fourth order Runge-Kutta
method (RK4). This tool also features a slider that allows the user to interact with the tool
and change the accuracy and precision of the drawn curves by changing the value of the step size.
The following equation is used as an example in this tool:
Which for the initial value of has the exact solution of:
The exact curve of this equation was drawn with a step size of ( equals ).
For small values of the step size, the curves are almost identical but as this value becomes
larger, the curves changes drastically; with the curve belonging the Euler’s method having the
most change and the RK4’s the least.