Researcher
K. N. Toosi University of Tech, Faculty of Mathematical Science
Biography
I am working as a researcher at the department of mathematics at K. N. Toosi University of Technology since 2013.
K. N. Toosi University of Technology, is a public university in Tehran, Iran, named after medieval Persian scholar Khajeh Nasir al-Din Toosi. The university is considered one of the most prestigious, government-sponsored institutions of higher education in Iran.
I have completed my MSc and Ph.D. at Sharif University of Technology and my undergraduate study at Isfahan University. My research interests lie in the area of Numerical Optimization and Computational Mathematics, specially those topics related to Machine and Deep Learning . A full survey of my researsh interests can be found in the Research Tab.
Academic Positions
-
2013 Present
Education & Training
-
Ph.D. 2012
Ph.D. in Applied Mathematics & Optimization
Sharif University of Tech
-
M.B.A.2007
Master's Degree in Optimization
Sharif University of Tech
-
B.A.2003
Bachelor's Degree in Applied Mathematics
University of Isfahan
Research Summary
My research activity is related to computational mathematics. In particular, i am very interested in large scale optimization. The subject of my master thesis was about designing and analyzing interior point algorithms for nonconvex optimization. Following this line of research, in my Ph.D. thesis, i proposed a new filter trust region algorithm for nonconvex problems. Nowadays, my focus of research is on developing new algorithms for large scale optimization, specifically, those arising from machine learning and image processing. Improving gradient-based algorithms like stochastic gradient method, modifying conjugate gradient algorithms and also second order methods working efficiently for large problems are on my agenda. Although i haven’t any research activities (articles) in discrete optimization, I am very interested in mixed integer programming and had many master students graduated in this area (see my CV). A part of my research area is about investigating tools from non-smooth optimization for solving discrete problems. I am also working on some numerical linear algebra algorithms in order to develop them by tools of numerical optimization.
Interests
- Computational Mathematic
- Numerical Optimization
- Numerical Linear Algebra
- Machine Learning
- Integer Programming
- Operation research
Research Projects
-
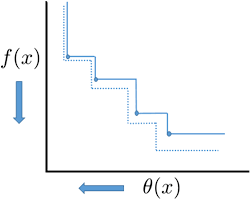
A new filter-trust-region algorithm for solving unconstrained and bound constrained optimization problems is introduced. Based on the filter technique introduced by Fletcher and Leyffer, it extends the existing technique to the fully general unconstrained optimization problems. The new algorithm is equipped with a new filter technique guarantying the finiteness of the filter size. Moreover, the worst case complexity of the filter size is introduced. We have shown the method is globally convergent to at least one second-order critical point, and numerical experiments indicate that it is very competitive with more classical trust-region algorithms.
-
Primal-dual interior methods for nonconvex nonlinear programming have recently been the subject of significant attention from the optimization community. Several different primal-dual methods have been suggested, along with some theoretical and numerical results. Although the underlying motivation for all of these methods is relatively uniform, there axe nonetheless substantive variations in crucial details, including the formulation of the nonlinear equations, the form of the associated linear system, the choice of linear algebraic procedures for solving this system, strategies for adjusting the barrier parameter and the Lagrange multiplier estimates, the merit function, and the treatment of indefiniteness. Not surprisingly, each of these choices can affect the theoretical properties and practical performance of the method. This thesis discusses the approaches to these issues that we took in implementing a specific primal-dual method.
Selected Publications
Filter by type:
Sort by year:
A modified conjugate gradient method for general convex functions
Journal PaperNumerical Algorithms. DOI:10.1007/s11075-022-01349-0
Abstract
The aim of this paper is to introduce a new non-smooth conjugate gradient method for solving unconstrained minimization problems. The proposed method is a member of a descent family of Dai-Liao conjugate gradient methods suitable for minimizing convex non-smooth objective functions. Under mild assumptions, our proposed method is globally convergent, and all search directions satisfy the sufficient descent condition. Numerical comparative results indicate that the new algorithm is efficient and outperform some exiting algorithms in this field.
On initial point selection of the steepest descent algorithm for general quadratic functions
Journal PaperComputational Optimization and Applications. Volume 82, Issue 2, 2022, Page(s) 329–360
Abstract
We prove some new results about the asymptotic behavior of the steepest descent algorithm for general quadratic functions. Some well-known results of this theory are developed and extended to non-convex functions. We propose an efficient strategy for choosing initial points in the algorithm and show that this strategy can dramatically enhance the performance of the method. Furthermore, a modified version of the steepest descent algorithm equipped with a pre-initialization step is introduced. We show that an initial guess near the optimal solution does not necessarily imply fast convergence. We also propose a new approach to investigate the behavior of the method for non-convex quadratic functions. Moreover, some interesting results about the role of initial points in convergence to saddle points are presented. Finally, we investigate the probability of divergence for uniform random initial points.
An efficient conjugate gradient method with strong convergence properties for non-smooth optimization
Journal Paper Journal of Mathematical Modeling, Volume , Issue , 2021, Pages
Abstract
In this paper, we introduce an efficient conjugate gradient method for solving nonsmooth optimization problems by using the Moreau-Yosida regularization approach. The search directions generated by our proposed procedure satisfy the sufficient descent property, and more importantly, belong to a suitable trust region. Our proposed method is globally convergent under mild assumptions. Our numerical comparative results on a collection of test problems show the efficiency and superiority of our proposed method. We have also examined the ability and the effectiveness of our approach for solving some real-world engineering problems from image processing field. The results confirm better performance of our method.
A new conjugate gradient method based on a modified secant condition with its applications in image processing
Journal PaperRAIRO-Oper. Res. Volume 55, Issue 1, 2021, Page(s) 167-187
Abstract
We propose an effective conjugate gradient method belonging to the class of Dai–Liao methods for solving unconstrained optimization problems. We employ a variant of the modified secant condition and introduce a new conjugate gradient parameter by solving an optimization problem. The optimization problem combines the well-known features of the linear conjugate gradient method using some penalty functions. This new parameter takes advantage of function information as well as the gradient information to provide the iterations. Our proposed method is globally convergent under mild assumptions. We examine the ability of the method for solving some real-world problems from image processing field. Numerical results show that the proposed method is efficient in the sense of the PSNR test. We also compare our proposed method with some well-known existing algorithms using a collection of CUTEr problems to show its efficiency.
A new conjugate gradient method with an efficient memory structure.
Journal Paper Computational and Applied Mathematics, Volume 38, Issue 2, 2019, pages 1-17.
Abstract
A new family of conjugate gradient methods for large-scale unconstrained optimization problems is described. It is based on minimizing a penalty function, and uses a limited memory structure to exploit the useful information provided by the iterations. Our penalty function combines the good properties of the linear conjugate gradient method using some penalty parameters. We propose a suitable penalty parameter by solving an auxiliary linear optimization problem and show that the proposed parameter is promising. The global convergence of the new method is investigated under mild assumptions. Numerical results show that the new method is efficient and confirm the effectiveness of the memory structure.
A LIMITED MEMORY CLASS OF CONJUGATE GRADIENT METHODS
Journal Paper PACIFIC JOURNAL OF OPTIMIZATION, Volume 15, Issue 3, 2019, Pages 457-475
Abstract
We combine the good properties of the linear conjugate gradient algorithm using an optimization problem, and introduce a new limited memory class of nonlinear conjugate gradient methods. This new class contains Dai-Liao family as a subclass. Using this idea, we propose a bound for the optimal Dai-Liao parameter. The global convergence of the new method is investigated under mild assumptions. The numerical comparing results indicate that the new method is efficient and competitive with CG-DESCENT.
A scaled conjugate gradient method for nonlinear unconstrained optimization.
Journal Paper Optimization Methods and Software, Volume 32, Issue 5, 2017, Pages 1095-1112.
Abstract
We propose a new optimization problem which combines the good features of the classical conjugate gradient method using some penalty parameter, and then, solve it to introduce a new scaled conjugate gradient method for solving unconstrained problems. The method reduces to the classical conjugate gradient algorithm under common assumptions, and inherits its good properties. We prove the global convergence of the method using suitable conditions. Numerical results show that the new method is efficient and robust.
A new efficient conjugate gradient method for unconstrained optimization.
Journal Paper Journal of Computational and Applied Mathematics, Volume 300, 2016, Pages 207-216.
Abstract
We propose a nonlinear conjugate gradient method for unconstrained optimization based on solving a new optimization problem. Our optimization problem combines the good features of the linear conjugate gradient method using some penalty parameters. We show that the new method is a subclass of Dai–Liao family, the fact that enables us to analyze the family, closely. As a consequence, we obtain an optimal bound for Dai–Liao parameter. The global convergence of the new method is investigated under mild assumptions. Numerical results show that the new method is efficient and robust, and outperforms CG-DESCENT.
An optimal parameter for Dai–Liao family of conjugate gradient methods.
Journal Papers Journal of Optimization Theory and Applications, Volume 169, Issue 2, 2016, Pages 587-605
Abstract
We introduce a new efficient nonlinear conjugate gradient method for unconstrained optimization, based on minimizing a penalty function. Our penalty function combines the good properties of the linear conjugate gradient method using some penalty parameters. We show that the new method is a member of Dai–Liao family and, more importantly, propose an efficient Dai–Liao parameter by closely analyzing the penalty function. Numerical experiments show that the proposed parameter is promising.
Two extensions of the Dai-Liao method with sufficient descent property based on a penalization scheme.
Journal Paper Bull. Comput. Appl. Math, Volume 4, 2016, Pages 7-19.
Abstract
To achieve the good features of the linear conjugate gradient algorithm in a recent extension of the Dai-Liao method, two adaptive choices for parameter of the extended method are proposed based on a penalization approach. It is shown that the suggested parameters guarantee the sufficient descent property independent to the line search and the objective function convexity. Furthermore, they ensure the global convergence of the related algorithm for uniformly convex objective functions. Using a set of unconstrained optimization test problems from the CUTEr library, effectiveness of the suggested choices are numerically compared with two other recently proposed adaptive choices. Results of comparisons show that one of the proposed choices is computationally promising in the sense of the Dolan-Moré performance profile.
An interior-point method for P*(kappa)-linear complementarity problem based on a trigonometric kernel function.
Journal Paper Journal of Applied Mathematics and Computing, Volume 48, Issue 1, 2015, Pages 111-128
Abstract
Recently, El Ghami (Optim Theory Decis Mak Oper Res Appl 31:331–349, 2013) proposed a primal dual interior point method for -Linear Complementarity Problem (LCP) based on a trigonometric barrier term and obtained the worst case iteration complexity as for large-update methods. In this paper, we present a large update primal–dual interior point algorithm for -LCP based on a new trigonometric kernel function. By a simple analysis, we show that our algorithm based on the new kernel function enjoys the worst case iteration bound for solving -LCP. This result improves the worst case iteration bound obtained by El Ghami for -LCP based on trigonometric kernel functions significantly.
A PROJECTED GRADIENT FILTER TRUST-REGION ALGORITHM FOR BOUND CONSTRAINED OPTIMIZATION.
Journal PaperPACIFIC JOURNAL OF OPTIMIZATION, Volume 10, Issue 1, 2014, Pages 229-242
Article
We present a filter trust-region algorithm for solving bound constrained optimization problems. The algorithm is an extension of our method recently proposed for unconstrained optimization to consider the bound constraints. The new algorithm combines the gradient projection method with the filter technique to generate non-monotone iterations. In contrast with the earlier filter algorithms, the new algorithm has the novelty to ensure the finiteness of the filter size. Global convergence to at least one first order critical point is established. Comparative numerical results on a set of test problems from the CUTEr collection show the algorithm is competitive and more efficient solely with respect to the filter size.
A modified two-point stepsize gradient algorithm for unconstrained minimization.
Journal Paper Optimization Methods and Software, Volume 28, Issue 5, 2013, Pages 1040-1050
Abstract
Based on a modified secant equation proposed by Li and Fukushima, we derive a stepsize for the Barzilai–Borwein gradient method. Then, using the newly proposed stepsize and another effective stepsize proposed by Dai et al. in an adaptive scheme that is based on the objective function convexity, we suggest a modified two-point stepsize gradient algorithm. We also show that the limit point of the sequence generated by our algorithm is first-order critical. Finally, our numerical comparisons done on a set of unconstrained optimization test problems from the CUTEr collection are presented. At first, we compare the performance of our algorithm with two other two-point stepsize gradient algorithms proposed by Dai et al. and Raydan. Then, numerical comparisons between the implementations of our algorithm and two conjugate gradient methods proposed by Gilbert and Nocedal, and Hestenes and Stiefel, and also...
A non-monotone trust region algorithm for unconstrained optimization with dynamic reference iteration updates using filter
Journal Papers Optimization, Volume 61, Issue 6, 2012, Pages 733-763
Abstract
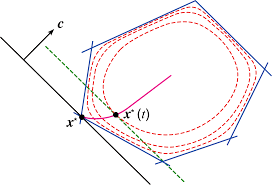
We present a non-monotone trust region algorithm for unconstrained optimization. Using the filter technique of Fletcher and Leyffer, we introduce a new filter acceptance criterion and use it to define reference iterations dynamically. In contrast with the early filter criteria, the new criterion ensures that the size of the filter is finite. We also show a correlation between problem dimension and the filter size. We prove the global convergence of the proposed algorithm to first- and second-order critical points under suitable assumptions. It is significant that the global convergence analysis does not require the common assumption of monotonicity of the sequence of objective function values in reference iterations, as assumed by the standard non-monotone trust region algorithms. Numerical experiments on the CUTEr problems indicate that the new algorithm is competitive compared to some representative non-monotone trust.
A filter trust-region algorithm for unconstrained optimization with strong global convergence properties
Journal Paper Computational Optimization and Applications, Volume 52, Issue 1, 2012, Pages 239-266
Abstract
We present a new filter trust-region approach for solving unconstrained nonlinear optimization problems making use of the filter technique introduced by Fletcher and Leyffer to generate non-monotone iterations. We also use the concept of a multidimensional filter used by Gould et al. (SIAM J. Optim. 15(1):17–38, 2004) and introduce a new filter criterion showing good properties. Moreover, we introduce a new technique for reducing the size of the filter. For the algorithm, we present two different convergence analyses. First, we show that at least one of the limit points of the sequence of the iterates is first-order critical. Second, we prove the stronger property that all the limit points are first-order critical for a modified version of our algorithm. We also show that, under suitable conditions, all the limit points are second-order critical. Finally, we compare our algorithm with a natural trust-region algorithm and the ..
Two effective hybrid conjugate gradient algorithms based on modified BFGS updates
Journal Paper Numerical Algorithms, Volume 58, Issue 3, 2011, Pages 315-331
Abstract
Based on two modified secant equations proposed by Yuan, and Li and Fukushima, we extend the approach proposed by Andrei, and introduce two hybrid conjugate gradient methods for unconstrained optimization problems. Our methods are hybridizations of Hestenes-Stiefel and Dai-Yuan conjugate gradient methods. Under proper conditions, we show that one of the proposed algorithms is globally convergent for uniformly convex functions and the other is globally convergent for general functions. To enhance the performance of the line search procedure, we propose a new approach for computing the initial value of the steplength for initiating the line search procedure. We give a comparison of the implementations of our algorithms with two efficiently representative hybrid conjugate gradient methods proposed by Andrei using unconstrained optimization test problems from the CUTEr collection.
A Modified Conjugate Gradient Method for Nonsmooth Optimization Problems
Conference Papers 51 Annual Mathematic Conference, 2021.
A New Conjugate Gradient Method for Unconstrained Optimization
Conference Papers The 12th International Conference of Iranian Operations Research Society, 2019.
A filter Barzilai-Borwein method
Conference Papers The 7th International Conference of Iranian Operations Research Society, 2014.
A globally convergent trust-region algorithm for unconstrained optimization using filter
Conference Papers The 4th International Conference of Iranian Operations Research Society, 2011.
Teaching
Currrent Teaching
-
Present 2021
Network Optimization
The purpose of this course is to examine in detail various strategies for solving network optimization problems such as Minimum cost flow problem, Shortest path problem, Maximum flow problem and so on.
-
Present 2021
Advanced Non-linear Optimization
The purpose of this course is to examine in detail various strategies for solving mathematical optimization problems from unconstrained to constrained.
Teaching History
-
2020 2018
Advanced Linear Optimization
The purpose of this Course is to examine in detail various strategies for solving linear programming problems and for extending the linear programming results to more general classes of mathematical programming problems.
-
2020 2018
Linear Optimization
A linear program is an optimization problem that seeks to minimize or maximize a linear function subject to a system of linear inequality and/or equality constraints. Applications of linear programs include transportation problems, flight scheduling, corporate planning, linear and nonlinear curve fitting, product mix, load balancing, production scheduling, inventory control, and many others. This course will cover the simplex method in detail, emphasizing both mathematical foundations as well as computational considerations for effective computer implementations.
-
2020 ----
Numerical Methods for Data Science
This is a survey course on numerical methods prominent in modern data analysis and machine learning. Building on basic methods of optimization and numerical linear algebra, the course will explore the role of numerical methods for treating several classes of data analysis problems, including low rank factorizations and completion of matrix data; function approximation by kernel methods; and analysis of data on graphs.
Software & Docs
Some Documents, Softwares and/or files provided during my research programs are available here. The content of this page is regularly updated.
Softwares and Compilers in used
- Matlab
- Maple
- Cplex
- C++
Docs & Files
-
CUTEr is an open source testing environment for optimization and linear algebra solvers. CUTEr provides a collection of test problems along with a set of tools to help developers design, compare, and improve new and existing test problem solvers.
A useful tutorial in farsi has been provided which is available from here. I am updating this tutorial, and the new version explains many interesting features like integrating CUTEr with other optimization packages. Please contact me if you require the new version.
Contact & Meet Me
I would be happy to talk to you if you need my assistance in your research or whether you need bussiness consulting. Though I have limited time, i am always ready to help and talk with students.
- office: 02177125070-300
- smfatemi@kntu.ac.ir
- Find me at Orcid
- Find me at Academia
- Find me at Publons
At My Office
You can find me at my office located at mathematic department of K. N. Toosi University of Technology.
I am at my office every day from 9:00 Am until 4:00 Pm, but you may consider sending an email or calling me to fix an appointment.
K.N.Toosi University of Technology Faculty of Mathematics Daneshgah Boulevard, Ehsan Street Exit, East Zeynoddin Highway, Tehran, Iran