| سعيد رضا صباغ يزدی | نرم افزارهاي علمي | صفحه اصلي | |||||
| نرم افزار
تحلیل مسائل علمی و
صنعتی نصير
|
|||||||
|
|
|
|
|
||||

معرفی نرم افزار حجم محدود تحلیل مسائل علمی و صنعتی
NASIR
سعيدرضا صباغ يزدي
دانشیار دانشکده مهندسی عمران
دانشگاه صنعتي خواجه نصير الدين طوسي
SYazdi@kntu.ac.ir
بهار 1386
پیشگفتار
براي تحليل مسائل علمي و صنعتي سه راه روابط جبري، اجراي آزمونهاي آزمايشگاهي و مدلسازي رايانه اي متداول و قابل کاربرد هستند. اما استفاده از روابط جبري به پديده هاي مستقل و مسائل با هندسه ساده محدود ميشود و آزمونهاي آزمايشگاهي علاوه بر اينکه با خطاهاي تغيير مقياس و اندازه گيري همراه هستند، اجراي آنها نسبتا پر هزينه ميباشد.
امروزه دسترسي به رايانه هاي پرقدرت و سريع، انجام عمليات محاسباتي سنگين بر روي مقادير قابل توجه اطلاعات را امکان پذير ساخته است. توسعه روشهاي عددي توانمند، حل همزمان معادلات ديفرانسيل حاکم بر پديده هاي موثر در يک مسئله واقعي مهندسي را ممکن نموده است. كاربرد مدلهاي كم هزينه عددی و مدلسازي پيچيدگيها و ابعاد هندسي مسائل واقعي را امکان پذیر ساخته است. از اينرو استفاده از نرم افزارهاي مختلف براي مدلسازي رايانه اي در بين مهندسان به سرعت رو به رواج است.
مدلهاي شبيهسازي رايانه اي از قابليت تحليل همزمان تمامي مشخصههاي پديده هاي مورد نظر در مسائل مرتبط با جريان سيالات و انتقال حرارت برخوردارند. اما در راه تدوين اين مدلها نيز مشكلاتي وجود دارد که تلاشهاي محققين براي غلبه بر آنها و ارتقاء دقت و توسعه كارائي آنها را بخود معطوف ساخته است. استفاده از نوع روش عددي و تكنيكهاي جديد مقوله تعيين كنندهاي برای دستيابي به انعطافپذيري، دقت، كارائي و توان مورد نظر ميباشد. همچنين بهبود كيفي روشهاي مدلسازي محيط هندسي مسئله و گسستهسازي حوزه حل از ديگر مسائل مهم و تعيين كننده در كيفيت شبيهسازي عددي است و تأثير زيادي نيز بر نتايج دارد. بطور كلي ميتوان گفت در صورتيكه تمام مراحل مدلسازي رايانهاي شامل منظور نمودن مدل رياضي جامع حاكم بر پديده، مدلسازي هندسه دقيق مسئله مورد نظر، تدوين الگوريتم حل عددي كامل و كارآمد و منظور نمودن صحيح شرايط مرزي لازم بدرستي صورت پذيرد، ميتوان نتايج قابل اعتمادي را انتظار داشت. از اينرو تحليل عددي مسائل مهندسي و محيط زيست همچنان بعنوان يکي از موضوعات چالش برانگيز در عرصه پژوهش مطرح است و کوشش در تهيه نرم افزارهاي مجهز به فنون جديد محاسباتي براي ارائه به کاربران بطور مداوم در جريان ميباشد.
پيشرفت در تدوين و توسعه نرم افزارها با ملاحظه مسائل مذكور در كنار دسترسي راحت و ارزان به رايانههاي توانمند باعث جلب توجه محققين بسياري در سطح جهان به شبيهسازي عددي شده و در ايران نيز اين روش مدلسازي علاقمنداني را جلب نموده است.
در گامي براي توسعه فنآوري شبيهسازي رايانهاي در كشور، نرم افزار حل حجم محدود مسائل مهندسي و محيط زيست مرتبط با جريان سيالات و انتقال حرارت با موفقيت در دانشکده عمران دانشگاه صنعتي خواجه نصيرالدين طوسي تکميل شده است. ماجولهای تحلیل حجم محدود برای شبیه سازی مسائل علمی و صنعتی در زمینه مهندسی عمران در قالب نرم افزار NASIR[1] توسعه یافته است. تعداد زیادی از این ماجولها با همکاری دانشجویان تحصیلات تکمیلی توسعه یافته و یا بکارگرفته شده اند.
زمینه های کاربرد
در حال حاضر این ماجولها برای مدلسازی مسائلی همچون موضوعات زیر مناسب میباشند:
1. تحلیل مسائل علمی و صنعتی در مدلسازی جریان میانگین عمقی با سطح آزاد (در کانالها و رودخانه ها)
2. تحلیل مسائل علمی و صنعتی در مدلسازی جریان میانگین عمقی با سطح آزاد (فرسایش، انتقال و ته نشست رسوب)
3. تحلیل مسائل علمی و صنعتی در مدلسازی جریان غیردائمی در لوله ها
4. تحلیل مسائل علمی و صنعتی در مدلسازی تولید و انتقال حرارت در بتن
5. تحلیل مسائل علمی و صنعتی در مدلسازی جریان در محیط متخلخل
7. تحلیل مسائل علمی و صنعتی در مدلسازی جریان دو بعدی باد و انتقال آلایندها
8. تحلیل مسائل علمی و صنعتی در مدلسازی جریان سه بعدی باد
شاید مناسب باشد که قبل از پرداختن به موارد آزمون و کاربرد نرم افزار NASIR در مسائل مهندسی عمران و محیط زیست، باختصار به مدل ریاضی (معادلات دیفرانسیل) استفاده شده برای هر مورد و کلیات حل حجم محدود آنها اشاره گردد.
مدل ریاضی جریان باد
با فرض ناچيز بودن تغييرات جرم حجمي هوا در سرعتهاي كمتر از يك سوم سرعت صوت، ميتوان معادله حاكم بر جريان را بصورت تراكم ناپذير در نظر گرفت. در جريانهاي با عدد رينولدز بالا، فرض اینکه لايه مرزي بسيار نازك نزديك به ديواره تقريبا به جسم بچسبد و به ناحيهاي كوچك و قابل اغماض نسبت به كل حوزه حل تبديل شود، تقريب مناسبي است.
در شكل تراكمناپذير معادلات
جمله مشتق زماني از معادله بقاي حجم حذف ميشود كه اين موضوع حل درگير آن را با
معادلات حركت با دشواري مواجه ميسازد. براي غلبه بر اين مشكل روش تراكم پذيري
مصنوعي پيشنهاد شده است[3] . اساس اين روش بر
پايه اضافه نمودن يك جمله مشتق زماني فشار مجازي، به معادلات بقاي حجم (پيوستگي)
ميباشد. اين امر موجب ميشود كه ارتباط عددي معادله پيوستگي با معادلات حركت برقرار
شود و حل درگير معادلات مذكور ممكن گردد. اين عبارت به كمك معادله حالت سيال با
جايگزيني مشتق زماني جرم حجمي![]() با مشتق زماني فشار شبيه سازي
شده است. در حل مسائل دائمي جمله تراكم پذيري مصنوعي اضافه شده در همگرائي محاسبات
به صفر گرائيده، معادله مورد نظر درنهايت نتيجهاي يكسان با معادلات تراكمناپذير
خواهد داشت.
با مشتق زماني فشار شبيه سازي
شده است. در حل مسائل دائمي جمله تراكم پذيري مصنوعي اضافه شده در همگرائي محاسبات
به صفر گرائيده، معادله مورد نظر درنهايت نتيجهاي يكسان با معادلات تراكمناپذير
خواهد داشت.
با استفاده از فرضيات ساده كننده فوق و نيز اعمال روش تراكم پذيري مصنوعي معادلات حاكم بصورت زير بيان ميشوند:
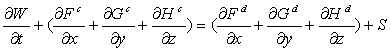
كه در آن
,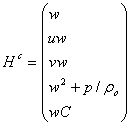 ,
,  ,
,  ,
, 
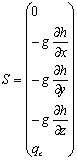 ,
, ,
,
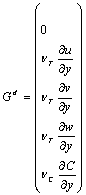 ,
,

در اين معادله![]() نماينده متغيرهاي وابسته و
نماينده متغيرهاي وابسته و![]() بردارهاي شار انتقالي كميت مورد بررسي
بردارهاي شار انتقالي كميت مورد بررسي![]() در سه راستاي
در سه راستاي![]() هستند.
هستند.![]() ،
،
![]() و
w مولفههاي سرعت و
و
w مولفههاي سرعت و![]() فشار، متغيرهاي وابسته مورد نظر ميباشند.
فشار، متغيرهاي وابسته مورد نظر ميباشند.
![]() جرم حجمي مورد نظر است.
جرم حجمي مورد نظر است.
![]() كه در روش تراكم ناپذيري
مصنوعي به معادلات افزوده شده است (
كه در روش تراكم ناپذيري
مصنوعي به معادلات افزوده شده است (![]() )،
شبيه به سرعت صوت در معادلات تراكمپذير، نقش ارتباط دهنده ميدان فشار را بين
معادلات پيوستگي و معادلات حركت در دستگاه معادلات ايفا ميكند. در معادلات
بالا h
نشانگر راستاي قائم و
g
شتاب ثقل ميباشد. در معادلات حركت و انتقال غلظت پارامترهاي
)،
شبيه به سرعت صوت در معادلات تراكمپذير، نقش ارتباط دهنده ميدان فشار را بين
معادلات پيوستگي و معادلات حركت در دستگاه معادلات ايفا ميكند. در معادلات
بالا h
نشانگر راستاي قائم و
g
شتاب ثقل ميباشد. در معادلات حركت و انتقال غلظت پارامترهاي
![]() بعنوان مجموع ضريب پخش
يا لزجت و پارامتر لزجت گردابه اي (جهت مدلسازي اثر آشفتگي) ميباشد.
بعنوان مجموع ضريب پخش
يا لزجت و پارامتر لزجت گردابه اي (جهت مدلسازي اثر آشفتگي) ميباشد.
برای محاسبه لزجت جریان آشفته، یک مدل آشفتگی زیر مقیاس شبکه[4](SGS)
استفاده شده است. در این مدل فرض می شود که گردابه های با اندازه بزرگتر از اندازه
شبکه توسط مدل عددی مورد تحلیل قرار می گیرند و مدل آشفتگی بایستی گردابه های
کوچکتر از اندازه شبکه را مورد لحاظ قرار دهد. لذا لزجت گردابه ای![]() را در مقیاس کوچک برای زیر شبکه
ها می توان از رابطه زیر، که شکل کلی مدل اسماگورنسکی برای جریانهای سه بعدی و
جریانهای تحت فشار است، بدست آورد:
را در مقیاس کوچک برای زیر شبکه
ها می توان از رابطه زیر، که شکل کلی مدل اسماگورنسکی برای جریانهای سه بعدی و
جریانهای تحت فشار است، بدست آورد:
![]()
![]() ,
,
![]()
.
![]() نیز
به صورت
نیز
به صورت ![]() تعریف شده است. ضریب
تعریف شده است. ضریب
![]() انتخاب شده
است.
انتخاب شده
است.
شرايط مرزي مورد استفاده براي حل معادلات بالا به دو دسته شرايط مرزي ديوار صلب (جدار غير قابل نفوذ) و مرزهاي عبور جريان دسته بندي ميشوند. در جدارهاي صاف ميتوان سرعت جريان را در جهت مماس بر مرز فرض نمود. در مرزهاي عبور جريان، با توجه به فرض تراكم ناپذيري (زير سرعت صوت بودن جريان)، بايستي مولفه هاي سرعت در مرزهاي ورودي جريان و فشار در مرزهاي خروج جريان اعمال شوند[5].
مدل ریاضی جريان غیرماندگار در لوله ها
معادلاتي كه برای جریان غیرماندگار در یک مجرای کشسان (عمدتا جهت تجزيه و تحليل مسائل ضربه قوچ) ارائه گرديده، بسيار متنوع ميباشد. در اين نظريه واقعيات زير، مد نظر قرار گرفته است:
1) جريان سيال هنگام وقوع ضربه قوچ به صورت ناپايدار يا غيرماندگار در
ميآيد و جريان اوليه ممكن است دائمي يا پايدار باشد، يعني:
![]() (Q: دبی جريان(متر مکعب بر ثانيه)، V:
سرعت جريان(متر بر ثانيه) و t
: زمان(ثانيه) می باشد).
(Q: دبی جريان(متر مکعب بر ثانيه)، V:
سرعت جريان(متر بر ثانيه) و t
: زمان(ثانيه) می باشد).
2) سيال به صورت خطي قابل تراكم بوده وخاصيت تراكم پذيري آن موجب ميشود كه با تغييرات فشار، جرم مخصوص سيال تغيير نموده و سيال به صورت يك محيط الاستيك عمل نمايد.
3) محاسبه افت انرژي جريان هاي ماندگار در حالت جريانهاي غيرماندگار نيز صدق مينمايد.
4) لوله جريان نيز به صورت خطي خاصيت كشساني دارد و در مقابل فشار، كرنش پذير ميباشد و از اين رو لوله افزايش قطر و طول پيدا ميكند.
با توجه به ساده سازيهای محاسباتی، معادله اندازه حرکت به شکل زير نوشته می شود:
![]()
كه درآن، D: قطرلوله(متر)، :V سرعت متوسط جريان(متر بر ثانيه)، x: امتداد طولی لوله، g: شتاب جاذبه(متر بر مجذور ثانيه)، H: مقدار هد آب(متر) و f :ضريب اصطکاک دارسی- وايسباخ می باشد.
همچنين با توجه به شکل (2-1) و ساده سازيهای محاسباتی، رابطه پيوستگی به شکل زير نوشته می شود:
![]()
در اين معادله: a: سرعت موج در لوله(متر بر ثانيه)، :V
سرعت متوسط جريان(متر بر ثانيه)، x: امتداد طولی لوله،
g: شتاب جاذبه(متر بر مجذور ثانيه)،
H: مقدار هد آب(متر) و![]() : زاويه
لوله با سطح افق(راديان) می باشد.
: زاويه
لوله با سطح افق(راديان) می باشد.
مدل ریاضی جريان آب با سطح آزاد
براي شبيهسازي جريان در كانالهاي باز تلاشهاي بسياري صورت پذيرفته است. بايستي توجه داشت كه سادهسازي يك پديده با حذف عوامل كم اهميت از اولين اصول برخورد با مسائل مهندسي است. تدوين يك مدل عددي با مدلسازي تاثيرات عمده در جريان مورد نظر آغاز ميشود. بعضي از عوامل فيزيكي در جريانات با شرایط خاص و در مجاري داراي هندسه ساده عمده و برخي ديگر قابل صرفنظر ميباشند. حذف عوامل كم اهميت مدلسازي پديده را ساده مينمايد. معادلات ميانگين عمقي (SWE) يكي از انواع متداول معادلات هيدروديناميك مورد استفاده در مدلسازي جريانهاي با سطح آزاد ميباشند.
اين معادلات بكمك انتگرالگيري از معادلات ناوير- استوكس سهبعدي از كف كانال تا سطح آب بدست ميآيند. در فرآيند انتگرالگيري از معادلات ناوير- استوكس فرض ميشود كه توزيع سرعت در عمق جريان يكنواخت است و فشار در جريان بصورت هيدرواستاتيك است، بعلاوه در بسياري از مسائل هيدروليكي ميتوان جريان را تراكمناپذير فرض کرد. در اينصورت معادلات ميانگين عمقي شامل يك معادله پيوستگي و دو معادله حركت جريان در سطح افق ميباشند. معادله دو بعدي انتقال و پخش يك غلظت مشخص را نيز ميتوان به مجموع معادلات افزود و شكل برداري معادلات را بصورت زير نوشت.
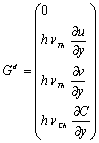
![]()
كه در آن
, 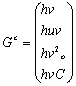 ,
,
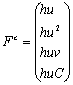 ,
, 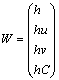
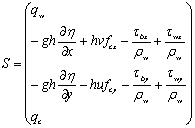 ,
,
 ,
,

كه در آن t برابر با زمان، x و y برابر با مؤلفههاي مختصات دكارتي،
![]() تراز
سطح آب، h برابر با عمق جريان و u و v برابر با سرعت جريان در جهات x و y ميباشند. در اينجا
تراز
سطح آب، h برابر با عمق جريان و u و v برابر با سرعت جريان در جهات x و y ميباشند. در اينجا
![]() نشانگر
دبي واحد سطح در جهت قائم (مجموع نشت و تراوش از بستر و تبخير و بارندگي از سطح)
ميباشد. در معادلات حركت پارامترهاي
نشانگر
دبي واحد سطح در جهت قائم (مجموع نشت و تراوش از بستر و تبخير و بارندگي از سطح)
ميباشد. در معادلات حركت پارامترهاي
![]() و
و
![]() بترتيب تنشهاي كلي ناشي از زبري بستر از اثر باد بر سطح جريان
و
بترتيب تنشهاي كلي ناشي از زبري بستر از اثر باد بر سطح جريان
و ![]() نيروي
موثر بر جريان در اثر چرخش زمين در جهات x و y ميباشند. پارامتر
نيروي
موثر بر جريان در اثر چرخش زمين در جهات x و y ميباشند. پارامتر
![]() بعنوان
مجموع ضريب پخش يا لزجت و پارامتر لزجت گردابه اي افقي (جهت مدلسازي اثرآشفتگي)
مبباشد. در معادلات بالا عبارات C يك غلظت مشخص (شوري يا آلاينده محلول
و يا مواد معلق) و
بعنوان
مجموع ضريب پخش يا لزجت و پارامتر لزجت گردابه اي افقي (جهت مدلسازي اثرآشفتگي)
مبباشد. در معادلات بالا عبارات C يك غلظت مشخص (شوري يا آلاينده محلول
و يا مواد معلق) و
![]() نشانگر
دبي واحد سطح آن غلظت در جهت قائم (مجموع چشمه و چاه) آن ميباشد.
نشانگر
دبي واحد سطح آن غلظت در جهت قائم (مجموع چشمه و چاه) آن ميباشد.
شرايط مرزي مورد استفاده براي معادلات بالا به دو دسته شرايط مرزي ديوار صلب (جدار غير قابل نفوذ) و مرزهاي عبور جريان دسته بندي ميشوند. در جدارهاي صاف ميتوان سرعت جريان را در جهت مماس بر مرز فرض نمود. مرزهاي عبور جريان با توجه به عدد فرود خود به دو نوع تقسيم ميشوند. اگر رژيم جريان زيربحراني باشد بايستي مولفه هاي سرعت در مرزهاي ورودي جريان و عمق در مرزهاي خروج جريان اعمال شود. اگر رژيم جريان فوقبحراني باشد بايستي مولفه هاي سرعت و عمق در مرزهاي ورودي جريان اعمال شود[2].
مدلهاي مختلفي براي بيان لزجت جریان آشفته
![]() بيان
شده اند. از مدلهای متداول، مدلهای جبری ميانگين عمقي میباشند. در اين مقدار لزجت جریان
آشفته
بيان
شده اند. از مدلهای متداول، مدلهای جبری ميانگين عمقي میباشند. در اين مقدار لزجت جریان
آشفته ![]() نيز به كمك رابطه زير قابل محاسبه است.
نيز به كمك رابطه زير قابل محاسبه است.
![]()
![]()
![]() سرعت
برشي بستر،
سرعت
برشي بستر، ![]() ضريب تجربي بين
ضريب تجربي بين
![]()
.Olson اين فرمول را بهترين راه براي محاسبه ضريب پخش ناشي از آشفتگي در رودخانه ها مي داند.
![]()
که در آن
![]() سرعت برشي بستر،
سرعت برشي بستر،
![]() عمق آب است. این فرمول بر
پایه رودخانه های طبیعی بنا نهاده شده و برای یک کانال مستقیم و عریض ضرایب متفاوتی
از 0.11 بدست خواهد آمد.
عمق آب است. این فرمول بر
پایه رودخانه های طبیعی بنا نهاده شده و برای یک کانال مستقیم و عریض ضرایب متفاوتی
از 0.11 بدست خواهد آمد.
مدل جبری دیگری براي تعيين لزجت جریان آشفته ،
![]() بشكل زير نوشته میشود.
بشكل زير نوشته میشود.
![]()
![]() ثابت ون كارمن برابر
0.41 ،
ثابت ون كارمن برابر
0.41 ، ![]() ضريب
ثابت برابر
ضريب
ثابت برابر ![]()
در مدل جبری دیگر که اصطلاحاً مدل با مقیاس شبکه ( (Sub
Grid Scale
شناخته میشود،
![]() بشكل
زير پیشنهاد شده است:
بشكل
زير پیشنهاد شده است:

![]() طول اختلاط ميانگين
عمقي و
برابر
طول اختلاط ميانگين
عمقي و
برابر ![]() میباشد.
میباشد.
مدلسازي جريان آب زیرزمینی
معادله غیردائمی حاکم بر پدیده تراوش در یک محیط متخلخل غیرهمگن ( Heterogeneou) و غیر همسان (Anisotropic) اشباع در حالت سه بعدی بصورت زیر قابل بیان است:

![]() ،
،![]() ،
،![]() ،
، ![]() و
و
![]()
که در آن عوامل مختلف عبارتند از:
h: ارتفاع نظیر فشار آب به متر (هد آب)
kz , ky , kx : ضرايب نفوذپذيري در جهات z , y , x
![]() :
با علامت مثبت: دبی در واحد حجم خروجی از حجم کنترل از طریق چاه (Sink) موجود در حوزه
:
با علامت مثبت: دبی در واحد حجم خروجی از حجم کنترل از طریق چاه (Sink) موجود در حوزه
با علامت منفی:دبی در واحد حجم ورودی به حجم کنترل از طریق چشمه (Source) موجود در حوزه
dV: حجم کنترل به ابعاد dx ، dy و dz (dV=dx.dy.dz)
Ss: ضریب ذخیره مخصوص میباشد. مفروضاتی که برای بدست آوردن این معادله در نظر گرفته شده است عبارتند از:
1) خاک کاملاً اشباع است.
2) آب و خاک غیر قابل تراکم هستند.
3) قانون دارسی حاکم است:
![]() که
در آن vx، vy و
vz
سرعت جريان در جهات x
، y و
z
می باشد.
که
در آن vx، vy و
vz
سرعت جريان در جهات x
، y و
z
می باشد.
در فرمول دارسی سرعت بصورت سرعت
ظاهری لحاظ شده است در صورتیکه مقدار سرعت واقعی بیشتر از سرعت ظاهری است (![]() که V’
سرعت واقعی و V سرعت ظاهری و Sy
ضریب آبدهی ویژه برابر تخلخل مؤثر خاک می باشد). علاوه بر این از قانون دارسی وقتی
می توان استفاده نمود که جریان در خاک بصورت لایه ای (Laminar
flow)
باشد و متلاطم (Turbulent)
نباشد. برای تعیین نوع جریان از عدد رینولدز استفاده می گردد (
که V’
سرعت واقعی و V سرعت ظاهری و Sy
ضریب آبدهی ویژه برابر تخلخل مؤثر خاک می باشد). علاوه بر این از قانون دارسی وقتی
می توان استفاده نمود که جریان در خاک بصورت لایه ای (Laminar
flow)
باشد و متلاطم (Turbulent)
نباشد. برای تعیین نوع جریان از عدد رینولدز استفاده می گردد (![]() که V
سرعت ظاهری، D قطر مؤثر ذرات خاک و
که V
سرعت ظاهری، D قطر مؤثر ذرات خاک و
![]() لزجت سینماتیک می
باشد). اگر
لزجت سینماتیک می
باشد). اگر ![]() باشد
جریان لایه ای بوده و می توان از قانون دارسی استفاده نمود. در صورتیکه
باشد
جریان لایه ای بوده و می توان از قانون دارسی استفاده نمود. در صورتیکه
![]() باشد
جریان در منطقه حد واسط بوده و با تقریب می توان فرمول دارسی را به کار برد. ولی
اگر
باشد
جریان در منطقه حد واسط بوده و با تقریب می توان فرمول دارسی را به کار برد. ولی
اگر ![]() باشد
قانون دارسی قابل استفاده نمی باشد. با توجه به اینکه در بیشتر حالات جریان آب در
خاک سرعت جریان کم می باشد، در این پایان نامه جریان از نوع لایه ای در نظر گرفته
شده و قانون دارسی حاکم می باشد.
باشد
قانون دارسی قابل استفاده نمی باشد. با توجه به اینکه در بیشتر حالات جریان آب در
خاک سرعت جریان کم می باشد، در این پایان نامه جریان از نوع لایه ای در نظر گرفته
شده و قانون دارسی حاکم می باشد.
مدل ریاضي توليد و انتقال دما در بتن
معادله زير براي بيان رياضي مسأله توليد و انتقال حرارت قابل كاربرد ميباشد:

![]() ،
،![]() ،
،
![]() ،
، ![]() و
و
![]()
در روابط فوق T دما و
![]() نرخ تغييرات
انرژي در واحد حجم (J/ m3 h) جسم جامد است.
نرخ تغييرات
انرژي در واحد حجم (J/ m3 h) جسم جامد است.
![]() را پخشيدگي حرارتي در
جهت
i
ميگويند. ρ
جرم حجمي (kg/m3 ) ، C گرماي ويژه (C ْJ /kg)،
را پخشيدگي حرارتي در
جهت
i
ميگويند. ρ
جرم حجمي (kg/m3 ) ، C گرماي ويژه (C ْJ /kg)،
![]() ضريب هدايت حرارتي در جهت i (CْW/m) يا (CْJ/hm)، و
ضريب هدايت حرارتي در جهت i (CْW/m) يا (CْJ/hm)، و
![]() نرخ توليد حرارت در واحد حجم سازه ميباشند.
نرخ توليد حرارت در واحد حجم سازه ميباشند.
در صورتيكه مدلسازي توليد و انتقال حرارت در بتن مد نظر باشد، براي محاسبه گرماي ناشي از هيدراسيون Q سيمان نسبت به زمان معادل te ، فرمول پيشنهاد شده توسط Rastrup قابل استفاده ميباشد. همچنين رابطة مورد استفاده جهت محاسبة زمان معادل te تابع سرعت واكنش ارائه شده توسط Rastrup، قابل كاربرد ميباشد. بنابراين رابطه مورد استفاده براي محاسبه نرخ حرارت زائي سيمان در مدلسازي تغييرات ناشي از گيرش بتن بصورت زير ميباشد.
![]()
در مسائل انتقال حرارت عمدتا يكي از دو نوع شرايط مرزي دريخله و يا طبيعي استفاده ميشود. براي اعمال شرايط مرزي دريخله متغير دما در مرزها اعمال ميشود. شرايط مرزي طبيعي از نوع اعمال گراديان دما در مرزهاي جسم جامد مي باشد و براي جسم بتني اجزاي آن شامل انتقال حرارت از سطح بتن از طريق همرفت(qc)، تابش خورشيد (qs) و پرتودهي حرارتي سطح بتن (qr) ميباشد[6].
حل احجام محدود
در اين مدل براي گسستهسازي معادلات از روش احجام محدود استفاده شده است. براي استفاده از اين روش محدوده حل به تعدادي زير محدوده مثلثي تقسيم ميشود و مقادير W در كره هاي شبكه (مرکز حجام كنترل متشكل از تجمع سلولها در يك گره) مجهول فرض ميشوند. معادله حاكم پس از انتگرالگيري بر روي حجم كنترل و استفاده از قضيه گرين بشکل روابط جبري زير تبديل ميشوند.
![]()
در اين رابطه![]() متغيري است كه از حل معادلات در مراکز احجام کنترل بدست ميآيد. پارامتر
متغيري است كه از حل معادلات در مراکز احجام کنترل بدست ميآيد. پارامتر![]() مقدار بدست آمده براي W
در گام زماني قبل است. متغير
مقدار بدست آمده براي W
در گام زماني قبل است. متغير
![]() برابر با مساحت حجم
کنترل است و
برابر با مساحت حجم
کنترل است و ![]() برابر
با تعداد يالهاي پديد آورنده هر حجم کنترل ميباشد. براي محاسبه مقادير
برابر
با تعداد يالهاي پديد آورنده هر حجم کنترل ميباشد. براي محاسبه مقادير
![]() و
و
![]() بايد از ميانگين
پارامتر ها در هر يال استفاده شود. مقادير
بايد از ميانگين
پارامتر ها در هر يال استفاده شود. مقادير
![]() و
و
![]() بايد در مركز يالهاي
مرزي حجم كنترل اصلي (با استفاده از احجام كنترل ثانويه در اطراف آنها) محاسبه
شوند. بدين ترتيب مدل احجام محدود بدست آمده ميتواند مقادير متغير W را در هر گام زماني بصورت صريح در گرههاي شبكه محاسبه نمايد.
بايد در مركز يالهاي
مرزي حجم كنترل اصلي (با استفاده از احجام كنترل ثانويه در اطراف آنها) محاسبه
شوند. بدين ترتيب مدل احجام محدود بدست آمده ميتواند مقادير متغير W را در هر گام زماني بصورت صريح در گرههاي شبكه محاسبه نمايد.
گام زماني مورد استفاده در هر
مرحله از محاسبات بايد متناسب با سرعت انتقال اطلاعات بين مراكز حجم كنترل مجاور
باشد. در حل مسائل مرتبط با جريان سيال سرعت انتقال اطلاعات را
ميتوان بكمك مقادير ويژه ماتريس ژاكوبين صورت همگن معادلات حاكم بدست آورد. در
مورد حل مسائل انتقال حرارت اين سرعت ميتواند متناسب با قابليت پخش حرارتي (![]() ) انتخاب گردد.
) انتخاب گردد.
لازم بذكر است كه در مواردي كه
معادلات حاكم بر مسئله شامل عبارتهاي انتقالي باشند (![]() و
و ![]() صفر
نباشند)، ناچيز بودن مقادير عبارتهاي نماينده استهلاكات فيزيكي رشد خطاهاي عددي
روند محاسبات روشهاي حل عددي صريح را با ناپايداري مواجه ميسازند. در چنين مواردي
اضافه نمودن عبارتهاي لزجت مصنوعي به معادلات انتقالي در ميرا نمودن نوسانات
وپايدارسازي روند حل موثر است. در مدل حاضر با تركيب نمودن عملگرهاي لاپلاسين و
بايهارمونيك با فرمول طراحي شده براي شبكههاي بيساختار و استفاده از ضرائب مناسب
بر اين مشكل غلبه شده است. اين فرمولبندي بگونهاي طراحي شده كه ضمن ميراسازي
نوسانات ناخواسته عددي كمترين صدمه را به دقت نتايج محاسباتي وارد نمايد[7].
صفر
نباشند)، ناچيز بودن مقادير عبارتهاي نماينده استهلاكات فيزيكي رشد خطاهاي عددي
روند محاسبات روشهاي حل عددي صريح را با ناپايداري مواجه ميسازند. در چنين مواردي
اضافه نمودن عبارتهاي لزجت مصنوعي به معادلات انتقالي در ميرا نمودن نوسانات
وپايدارسازي روند حل موثر است. در مدل حاضر با تركيب نمودن عملگرهاي لاپلاسين و
بايهارمونيك با فرمول طراحي شده براي شبكههاي بيساختار و استفاده از ضرائب مناسب
بر اين مشكل غلبه شده است. اين فرمولبندي بگونهاي طراحي شده كه ضمن ميراسازي
نوسانات ناخواسته عددي كمترين صدمه را به دقت نتايج محاسباتي وارد نمايد[7].
جمع بندي
در بخشهاي ضمیمه آزمونهاي کارایي و دقت نرم افزار تحليلگر حجم محدود مسائل علمي و صنعتي ([1]NASIR) براي شبيه سازي مسائل متداول سيالات در مهندسي عمران و محیط زیست در محيطهای داراي پيچيدگيهاي هندسي با مورد آزمون و کاربرد قرار گرفت. کاربردهاي مذکور با آزمونهاي شاهد مورد ارزيابي قرار گرفت و نتايج مطلوب نرم افزار تحليلگر حجم محدود صحت عملکرد و کارآمدي آنرا مورد تائيد قرار ميدهد. در ذیل هر آزمون و یا کاربرد، بهنمونه ای از مقالات منتشر شده در مورد جزئیات و فنون بکار گرفته شده در مدلسازی عددی و نحوه بررسی دقت و کارائی نرم افزار مذکور در مدلسازی مسائل مهندسي عمران اشاره شد. انعطاف پذيري، كارایي، توان، دقت مطلوب نرم افزار تهيه شده دلگرمي لازم را براي توسعه و تكميل آن جهت استفاده براي مسائل كاربردي و تحقيقاتي فراهم ميسازد.